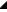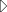Raises a number to a power. For example, you can use this function to square the number 2 to get the result of 4.
NewNumber := POWER(Number, Power) |
Parameters
- Number
- Type: Integer or Decimal The number you want to raise exponentially. This number is the base in the exponential function.
- Power
- Type: Integer or Decimal The exponent in the exponential function.
 Property Value/Return Value
Property Value/Return Value
Type: Decimal
The result of raising Number by Power.
 Example
Example
This example requires that you create the following variables and text constants in the C/AL Globals window.
| Variable name | DataType |
|---|---|
Number1 | Decimal |
Power1 | Decimal |
Result1 | Decimal |
| Text constant name | Constant value |
|---|---|
Text000 | %1 raised to the power of %2 = %3 |
 Copy Code Copy Code | |
|---|---|
Number1 := 64; Power1 := 0.5; Result1 := POWER(Number1, Power1); MESSAGE(Text000, Number1, Power1, Result1) | |
On a computer that has the regional format set to English (United States), the first message window displays the following:
64 raised to the power of 0.5 = 8
This example shows that raising a number to the power of 0.5 corresponds to the square root of the number.
 Example
Example
This example shows a typical use for the POWER function.
If a principal amount P is deposited at interest rate R and compounded annually, then at the end of N years, the accumulated amount (A) is:
A = P(1 + R)N
For example, you put LCY 2800 into a bank account that pays 5 percent, which is compounded quarterly. To determine what the amount will be in eight years, you must consider:
N = 32 payment periods (8 years times 4 quarterly periods)
R = 0.0125 per period (5 percent divided by 4 quarterly periods)
The accumulated amount A is:
A = LCY 2800(1 + 0.0125)32 =LCY 2800(1.4881) = LCY 4166.77
If a principal amount P is deposited at the end of each year at interest rate R (in decimal notation) compounded annually, then at the end of N years, the accumulated amount is:
A = P[((1 + R)N - 1)/R]
This is typically called an annuity.
For example, you have an annuity in which a payment of LCY 500 is made at the end of each year. The interest on this annuity is 4 percent, which is compounded annually. To determine what the annuity will be worth in 20 years, you must consider:
R = 0.04
N = 20
The amount of the annuity A will be:
A = LCY 500[((1 + 0.04)20 - 1)/0.04 = LCY 14,889.04
This example requires that you create the following variables and text constants in the C/AL Globals window.
| Variable name | DataType |
|---|---|
P | Decimal |
R | Decimal |
N | Decimal |
A | Decimal |
FormatString | Text |
| Text constant name | Constant value |
|---|---|
Text000 | Principal $%1 at a 5 percent interest rate is compounded quarterly.\ |
Text001 | (Rate = %2)\ |
Text002 | The amount after %3 years = $%4. |
Text003 | Principal $%1 is deposited at the end of each year at a 4 percent interest rate, compounded annually.\ |
Text004 | (Rate = %2)\ |
Text005 | The amount after %3 years = $%4. |
 Copy Code Copy Code | |
|---|---|
FormatString := '<Precision,2><Standard Format,1>'; // Example 1 P := 2800; R := 0.0125; N := 32; A = P * (POWER(1 + R, N)); MESSAGE(Text000 + Text001 + Text002, P, R, N, FORMAT(A,0,FormatString); // Example 2 P = 500; R = 0.04; N = 20; A = P * ((POWER(1 + R, N) - 1)/R); MESSAGE(Text001, P, R, N, FORMAT(A,0,FormatString)); | |
On a computer that has the regional format set to English (United States), the first message window displays the following:
Principal $2,800 at a 5 percent interest rate is compounded quarterly.
(Rate = 0.0125)
The amount after 32 years = $4166.77.
The second message window displays the following:
Principal $500 is deposited at the end of each year at a 4 percent interest rate, compounded annually.
(Rate = 0.04)
The amount after 20 years = $14889.04.